Matlab fmincon的用法

%問題描述
假設你要處理一個最佳化問題，目標函數是ObjFun(X1,X2,X3,....,Xn)其中有變數 X1,X2,X3,....,Xn，這些變數可以用向量或是單一的純量，看需求而定。
則你要的就是min ObjFun(X1,X2,X3,....,Xn)
限制在
            A*X1 =B                        ----------------------------------(1)
Aeq*X1=beq;                            ----------------------------------(2)
       NonlineConFun(X1)          ----------------------------------(3)
     NonlineFun(X1)=0;              ----------------------------------(4)
%========================================================
如果你有限制式(1) (2) (3) (4)其中之一，則就要用到fmincon 不然就單純使用fminsearch
，這些限制式可以全部都用到也可以只用到其中一個兩個或三個限制式，如果沒有使用就是以A=[]取代，如下面的寫法，則最佳化方程式就可以正確執行了。
簡單抽象範例如下。 另外一篇在提供實際執行案例。
%==============初始值=====================================
options = optimset('Display','iter','TolFun',1e-7,'MaxFunEvals',10000);
%options 設定最佳化在執行時候的選項，
%詳細請在Matlab的Help輸入 Optimization Options  Reference
nonlcon=[];沒有非線性項的初始值
A=[];
b=[];
Aeq=[];
beq=[];
lb=[0 0 0];%假設函數是要變數X1是一個1*3的向量，X1變數的下界
ub=[100 100 100];X1變數的上界
x01=[1 0 0] 問題函數X1的初始值
%==============初始值=====================================
%最佳化函數沒有非線性項 nonlcon
OptValue1 = fmincon(@(X1) ObjFun(X1,X2,X3,....,Xn),x01,A,b,Aeq,beq,lb,ub,nonlcon,options)
%最佳化函數有非線性項 Fun_non
OptValue2= fmincon(@(X1) ObjFun(X1,X2,X3,....,Xn),x01,A,b,Aeq,beq,lb,ub,@Fun_non,options);


%@ 表示handle 就是以該變數的記憶體位置來運算數值結果，是抽象的概念。
%@Fun_non 表示該限制式與@(X1) ObjFun(X1,X2,X3,....,Xn) 的變數是一樣的值，也就是說X1=向量A，則@Fun_non 也要帶入向量A。

matlab 計算程式運算時間

matlab中有兩個計算程式CPU的耗費時間方法

第一個為最常用的tic，toc。
tic
運算程式
toc

實際例子 Example

tic

n=1000;

A=rand(n,n);

b=rand(n,1);

x = A\b;

toc

結果 Result

Elapsed time is 0.069797 seconds.

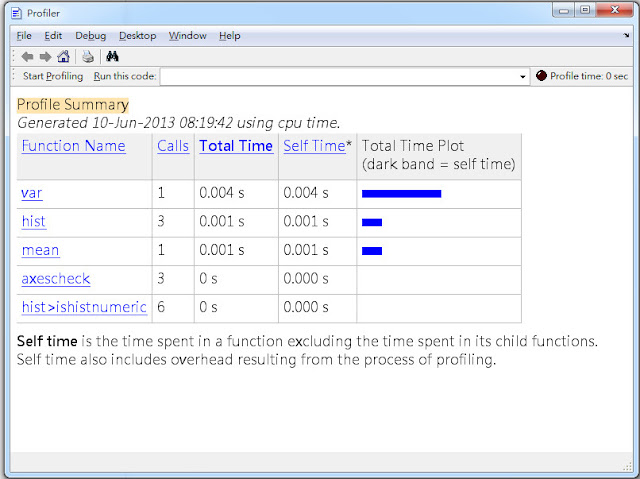
第二個為 profile，對於整個執行過程的函數做個別計算CPU的耗費時間

實際例子 Example

profile on    %執行函數運算時間計算

x1 = randn(1,100);

x2 = randn(1,100);

x3 = randn(1,100);

HistValuex1 = hist(x1);

HistValuex2 = hist(x2);

HistValuex3 = hist(x3);

mean(x1)

var(x1)

profile viewer     %顯示計算時間

p = profile('info');%定義計算時間所暫存的記憶體位置

profsave(p,'profile_results')   %將計算時間存檔

結果 Result

CDS 報價 (市場流動性高) Last Quote for the most Liquid Credit Default Swaps

Markit Group has developed this free 

"Last Quote for the most Liquid Credit Default Swaps" 

pricing report to address a public interest in CDS prices.

http://www.markit.com/cds/most_liquid/markit_liquid.shtml

Markit 將市場上流動性較高的CDS，把每日的最後一筆報價公開出來。

如果有需要的可以直接點連結

Matlab 模擬股價 以及 選擇權價格 Simulate Stock Price and Option Value

             S_0 = 100
          sigma = 0.4;
                  r = 0.012;
     dividend = 0.05;%股利
        Start_t  =  0;
Maturity_T  =  5;
          Tday  =  360;
               dt  =  1;
  StrikePrice = 80;
                t_i = (0:dt:Maturity_T*Tday)/Tday;
        PathM  = 10000; %路徑
          SizeM = size(t_i,2);
S(1:PathM,1)  =  S_0;
               h  =  dt/Tday;
for j=2:SizeM
          S(1:PathM,j)=S(1:PathM,j-1)+r*S(1:PathM,j-1).*repmat((t_i(1,j)-t_i(1,j-1)),PathM,1)+sigma*S(1:PathM,j-1).*repmat(sqrt(h),PathM,1).*randn(PathM,1);
end
%模擬的值  
    CallValue=mean(max((S(:,SizeM)-StrikePrice),0))*exp(-r*Maturity_T)
     PutValue=mean(max((StrikePrice-S(:,SizeM)),0))*exp(-r*Maturity_T)
%Matlab內建的公式值    
  [Call, Put] = blsprice(S_0, StrikePrice, r, Maturity_T, sigma, 0)

MikTex + Texmaker UTF8 中文latex

設定很簡單下載Miktex 淨安裝 選擇全部下載之後再選擇
http://mirrors.ctan.org/systems/win32/miktex/setup/setup-2.9.4503.exe

先選擇下載 下載完之後到下載目錄找到setup.exe然後直接安裝就可以。

選擇完整下載，這樣比較省事可以不用一直安裝新的東西總容量大概1G

選擇下載伺服器 通常會選擇日本因為台灣的很慢但看個人喜好 

 選擇下載資料夾 只要知道放在哪一個資料夾就好

下載完之後到該下載目錄找到setup.exe然後一直按下一步下一步安裝就可以安裝好

下載Texmaker編輯器
http://www.xm1math.net/texmaker/download.html
以前都使用Winedt但現在比較建議使用 Texmaker因為是免錢的。
(當然其他的PDF閱讀軟體, PS軟體也請自行下載安裝)
下載 Ghostscript 以及 Gsview
http://pages.cs.wisc.edu/~ghost/
 http://pages.cs.wisc.edu/~ghost/gsview/get50.htm
選擇你要的版本 並且一直按yes yes yes 安裝好就可以。


使用 Texmaker 就直接打開texmaker就好不用任何設定
從下一行開始複製貼上

% !Mode:: "TeX:UTF-8"

\documentclass[12pt]{article}

\usepackage{amsmath}

\usepackage{CJKutf8}

\usepackage{amssymb}

\usepackage[round]{natbib}

\title{Valuation}

\date{}

\author{•}

\begin{document}

\begin{CJK}{UTF8}{bsmi}

%\begin{frontmatter}

\maketitle

中文Latex

\end{CJK}
\end{document} 

到此要選擇存檔,因為檔頭已經自動存成UTF8 (多這一行的緣故% !Mode:: "TeX:UTF-8")
存檔類型選擇:UTF8(有包含:)
存檔名稱XXXX.tex(XXXX任意決定).
然後按Latex的編譯選項就可以看到 選擇Latex編譯出來 預設是以Dvi看，
如果想轉成PDF請選擇PdfLatex

第二種方法 經由三個程序先編譯 Latex 在編譯選項 Dvi->PS 最後選擇PS->PDF
第三種方法 可以直接選擇Dvi->PDF 都可以將Latex轉換成PDF

最後的結果就會顯示如下

中文Latex

Matlab 的GPU與平行計算 (GPU and parfor) Matlab Parallel Computing

Matlab Parallel Computing
平行計算已經在資訊界發展很久從電腦式的分散系統，到現在因為多核心處理器的原因，可以在個人電腦上簡單的使用平行運算，在MATLAB裡面最主要的兩個平行計算一個是GPU計算一個是parfor，兩者的目的都是為了減少計算時間，但所運行的環境不一樣。

MATLAB在GPU的使用一定要有一塊NVIDIA的顯示卡，ATI可以嗎? (在MATLAB的發展沒有比NVIDIA好)
首先要在這裡查詢你的顯示卡是不是適合
https://developer.nvidia.com/cuda-gpus
選擇的顯示卡記憶體要越大越好，因為GPU的運算是利用顯示卡以及他的記憶體在做運算的，所以顯示卡的記憶體越大越不會out of memory。


ParFor的使用就是運用電腦的多核心來計算，所以核心數目越多就可以越分散，可以把一個核心當成一台電腦來看有八核心就是八台電腦在運算。

如何分辨要使用ParFor跟GPU，
簡單的分類如果你的程式需要用到很多for而且每一個for的使用都是一段連續的那就可以考慮使用ParFor的運算 舉一個例子

你可能在切蛋糕 蛋糕都是一樣的 但有一百個 所以你就可以把蛋糕分給4個人 每一個人切25個 這就是使用parfor的概念 原本一個人重複切100個 丟給四個人切 一個人切25個就又快又好了。


而GPU的使用是在於你有頗多的計算步驟，顯示卡的運算環境又可以容納你所指配的變數大小，那這時候丟到GPU計算就會顯示出效果，比如說你要算20個運算符號的方程式，這時侯就可以考慮丟到GPU裡面去算。

或是 有兩個 200*200的矩陣大小要做反矩陣的運算 這時候GPU就是最好的計算環境。

計算時間成本，無論你使用GPU或是PARFOR都有計算成本，PARFOR在事前需要打開MATLABPOLL多核心執行指令，GPU需要將變數從電腦的記憶體輸送到顯示卡的記憶體，因此如果計算量不是很大是不需要用這兩個工具來做運算的，尤其在GPU運算更不能夠重複的搬進搬出記憶體，這樣耗費的時間會遠比你計算的時間多很多。

Matlab的最佳化函數介紹

Matlab的最佳化是最多人所使用的功能之一，舉凡數學中的解N元一次方程式，或是最大值最小值都會用到，在到商學院中的回歸分析，以及投資組合最佳化，效率前緣等都會用到，所以在此簡單的介紹Matlab常用的最佳化函數
最佳化的主要運用到的語法應該分為 單變數以及多變數的最佳化 還有線性以及非線性，再來細分可以分成有限制函數的最佳化以及沒有限制函數，最後最常用的就是解根的方程式fzero

1. fminbnd : 在固定區間中找出單變數的最小化方程式。
2. fminsearch: 如果要求解兩個未知數且是沒有限制函數的最佳化方程式就要用這一個。
3. fzero: 單變數找根的最佳化方程式，舉一個例子就是x^2-5x+4=0求解x的時候需要用到的。
4. fmicon: 用在有限制是底下時候非線性的多變數最佳化。
5. fminmax: 在求取最小最大化的條件所需要用到的。
6. fminucn:在沒有限制式底下的多變數最佳化求解。
7. fseminf: 多變數中變數又可以區分成兩種空間，比如說有一條方程式a1x1+a2x2=c 針對 a1 a2 以及x1 x2都需要求最佳化的時候，其中有一類變數是有限定區域的。
8. linprog: 線性最佳化，這是最常用的之一，就是在解N元一次方程式的最佳解。
9. quadprog:可以寫成Quadratic的函數就可以用這一個方程式來求解。